All measurements, be they chemical, microbiological or physical, carry some uncertainty. Testing laboratories have, by necessity, become familiar with the concept of measurement uncertainty. Their clients – who must interpret and act on the basis of uncertain measurements – may be less familiar. The intention of this fact sheet is to explain why it is necessary to understand measurement uncertainty, the basic fundamentals of what it is, how its calculation can differ between laboratories, and its practical implications. It thus complements our guideline on microbiological measurement uncertainty, which is primarily aimed at testing laboratories. We also offer bespoke training in this.

Introduction

Since 1999 ISO 17025 "General requirements for the competence of testing and calibration laboratories" has required that testing laboratories "shall have and shall apply procedures to estimate the uncertainty of measurement" (ISO 1999;ISO 2005). At Campden BRI we frequently advise clients' laboratories on this.

Until quite recently – at least in the food and drinks industry – most users of laboratory results have been unconcerned by measurement uncertainty, leaving it as a technical topic to be handled by their laboratories. However, ISO 17025 requires laboratories to accompany a result with a measurement uncertainty estimate:

• when it is relevant to the validity or application of the test results
• when a client's instruction so requires, or
• when the uncertainty affects compliance to a specification limit.

This means you may be presented with uncertainty on a result even when you haven't asked for it, like this example:

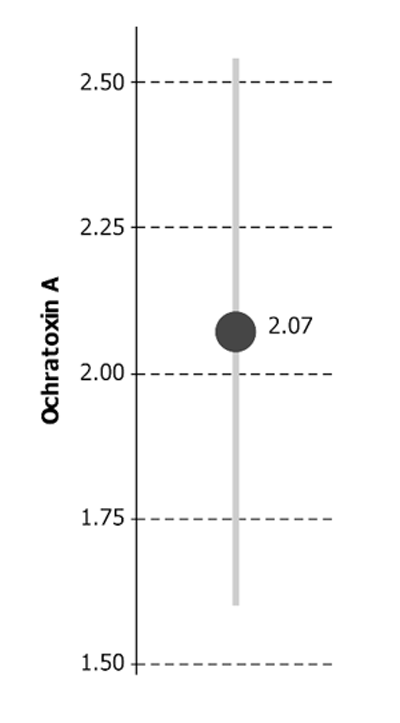
Ochratoxin A = 2.07 μg/kg ± 0.47 μg/kg*
* The reported expanded uncertainty is based on a standard uncertainty multiplied by a coverage factor of k = 2 to give a confidence level of approximately 95%

The reported result (e.g. 2.07) is the laboratory's best estimate of the 'true' value. But no one expects it to be exactly correct, raising the question of what the 'true' value might be. The definitive "Guide to the expression of uncertainty in measurement", known as "the GUM" (Joint Committee on Guides in Metrology 2008) studiously avoids the idea of a true value, defining uncertainty of measurement as a "parameter, associated with the result of a measurement, that characterizes the dispersion of the values that could reasonably be attributed to the measur and". But, at least informally, we can consider the 'expanded uncertainty' (e.g. ± 0.47) as a reasonably credible range for the true value.

This short note discusses the interpretation of such uncertain results under two headings:

• 'Quality' of the result: What does the uncertainty say about the laboratory?
• Compliance: Does the uncertain result imply compliance or failure?

'Quality' of the result

It is tempting to see Uncertainty of Measurement as failure to properly perform a test, and smaller stated measurement uncertainty (MU) as evidence of better performance. But it's not as simple as that…

The definition of MU (above) contains that slippery word "reasonably". Different people can attribute different values, all reasonable, giving different stated MUs for the same performance.

This was recognised as long ago as 2004: "the current lack of standardisation has caused the estimated measurement uncertainties to vary widely, even for the simplest determinations" (Visser 2004). Solfrizzo et al. (2009) recognised that " a large variability of measurement uncertainty … was probably due to non-harmonized interpretation of the term". Very recently (Breidbach et al. 2010) noted inconsistent MU estimations and that "Clients will more likely than not choose laboratories with narrower MU", even though narrower MUs might reflect less stringent MU evaluation rather than better measurement.

So you can't compare MUs between laboratories unless you know how they were calculated; the larger MU may result from more careful uncertainty estimation. In fact, you can't really interpret an MU value at all without some information on how it was calculated!

There is still disagreement among mathematicians, statisticians, and metrologists on the details of calculating an MU, so we can't expect substantial standardisation soon. And some of those details are so technical that non-specialists can't be expected to assess them.

One relatively simple aspect is important enough and should be checked: which 'components of uncertainty' have been included. The ISO 17025 requirements that "all uncertainty components which are of importance in the given situation shall be taken into account" and that "the form of reporting of the result does not give a false impression of the uncertainty" are so open to interpretation that you cannot take for granted which components have or have not been included. For example, in microbiology some guidance (European Co-operation for Accreditation 2002) suggests that within sample variation be excluded while other guidance (ISO 2009) takes it into account.

However, ISO 17025 requires that "the laboratory shall at least attempt to identify all the components of uncertainty", so they should be able to tell you which components they have included. If uncertainty of measurement matters to you, you should satisfy yourself that relevant uncertainty components are included – or at least be aware of those which are not.

Compliance

If you've paid a laboratory for a measurement you probably want to use it (!), which usually means comparison with some requirement or specification. Before MU that was easy, the value was either above or below any limit. But MU brings the possibility of values spanning a limit, as in this figure from (ILAC 2009).

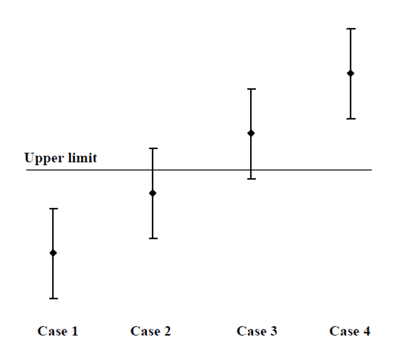
Clearly Case 1 complies with the Upper limit and Case 4 breaches it. But what about Case 2 and Case 3? It is more likely that Case 2 complies than fails, and that Case 3 fails rather than complies, but there is inadequate confidence in those conclusions.

In an ideal world the specification would take account of MU, clearly stating that the test result, extended by the uncertainty at a given level of confidence, should meet the limit – but not many specifications do!

Passing the buck to the laboratory won't help. If you tell them about the limit then ISO 17025 requires that the test report include "where relevant, a statement of compliance/non-compliance with requirements and/or specifications". But, as the one most familiar with the background and implications, you should really be making the final decision! In any case, the laboratory is likely to follow guidance, e.g. (ILAC 2009), and give a 'don't know' answer such as (for Case 2) "It is not possible to state compliance using a 95% coverage probability for the expanded uncertainty although the measurement result is below the limit".

One approach (ISO 2003) in the event of a 'don't know' is to replicate the test, effectively narrowing the MU interval. But reasonable replication gives relatively little narrowing, so a 'don't know' conclusion is still likely.

Another approach is to reduce the 'coverage probability', that is the confidence associated with uncertainty interval. Usually the 'expanded uncertainty' has an associated confidence level of approximately 95%, which can (very loosely!) be thought of as a 95% chance that the MU interval includes the 'true' value. As the confidence gets lower the MU interval gets narrower, so it may no longer span the limit. If, for your purposes, a lower confidence is acceptable this might be a solution.

In the extreme, when the confidence is 0% the MU interval disappears and the assessment of compliance is made on the test r esult, taking no account of MU. According to (APLAC 2006) "This is often referred to as shared risk since the end-user takes some of the risk...". It may be appropriate when the limit forms part of a trading agreement, but then a more transparent approach would be to write MU handling into the agreement.

When the limit forms part of a regulatory specification, probably neither a 'don't know' nor a reduced confidence is acceptable. In that case, the appropriate interpretation depends on who is asking! From a regulatory officer's viewpoint, Case 3 is unlikely to give adequately strong evidence of a breach, so is likely to be treated as compliance. From a producer's viewpoint, Case 2 cannot be taken as contribution much to a 'due diligence' defence, so will probably be treated as failure.

Conclusions

So Uncertainty of Measurement isn't simple to interpret; you wouldn't be alone if you thought it didn't add much to the more precisely defined precision and bias. But ISO 17025 means you may receive results with an associated MU.

Before relying on an MU, ensure you know how it was estimated – at least that it includes all relevant uncertainty components. Don't assume that a smaller MU means a better measurement.

When assessing compliance, ideally specify the handling of MU as part of the limit – e.g. in a trade agreement. For regulatory limits, enforcement authorities are likely to give the benefit of the MU doubt to the producer's side, but producers should 'play safe' in assessing their own compliance.

References

APLAC 2006, Method of Stating Test and Calibration Results and Compliance with Specifications TC 004.

Breidbach, A., Bouten, K., Kroeger, K., & Ulberth, F. 2010, "Capabilities of laboratories to determine melamine in food - results of an international proficiency test", Analytical & Bioanalytical Chemistry, vol. 396, no. 1, pp. 503-510.

European co-operation for Accreditation 2002, Accreditation for Microbiological Laboratories, European co-operation for Accreditation, EA-04/10rev02.

ILAC 2009, Guidelines on the Reporting of Compliance with Specification ILAC-G8:03/2009.

ISO 1999, General requirements for the competence of testing and calibration laboratories, International Organisation for Standardisation, Geneva, ISO/IEC 17025.

ISO 2003, Statistical methods - Guidelines for the evaluation of conformity with specified requirements - Part 1: General principles, International Organisation for Standardisation, Geneva, ISO 10576-1.

ISO 2005, General requirements for the competence of testing and calibration laboratories, International Organisation for Standardisation, Geneva, ISO/IEC 17025:2005.

ISO. Microbiology of food and animal feeding stuffs. Guidelines for the estimation of measurement uncertainty for quantitative determinations. ISO/TS 19036:2006+A1:2009. 2009. Ref Type: Statute

Joint Committee on Guides in Metrology 2008, Evaluation of measurement data — Guide to the expression of uncertainty in measurement, Bureau International des Poid et Mesures, Paris, France, JCGM 100:2008.

M. Solfrizzo, A. J. Alldrick, and H. P. Egmond. The use of mycotoxin methodology in practice: a need for harmonization. Quality Assurance & Safety of Crops & Foods 1, (2):121-132, 2009.

Visser, R. 2004, "Measurement uncertainty: practical problems encountered by accredited testing laboratories", Accreditation and Quality Assurance, vol. 9, no. 11, pp. 717-723.